In the article Worst-case Tolerance Stack-up Analysis you read about the worst-case or linear stack-up analysis. Such an analysis assumes that all dimensions in the tolerance chain have worst-case deviations form their nominal value. A statistical tolerance stack-up analysis takes the probability of a tolerance value and the combination of tolerances into account. It turns out that the probability of a worst-case combination is negligible for already a small number of parts. Let’s take a look at the following example.
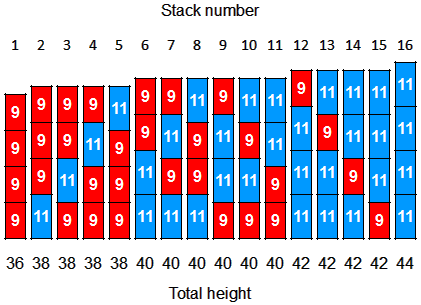
Suppose that you make a stack of 4 identical parts and you want to analyze the total height of the stack. The parts have a height specification of 10 +/-1. Now assume that all the parts have a worst-case deviation and are either 9 (part ‘9’) or 11 (part ’11’) high (any dimension, mm, inch, meter, et cetera). With just 4 parts it is still doable to write down all possible combinations.
So, there are 16 possible combinations. The probability of an extreme thickness is 2/16 = 12.5%. If for instance only the highest stack is problematic than this probability is only 6.25%. Notice that this is an extreme distribution of tolerances with a low probability itself. In practice the probability of an extreme height is very low.
It is clear that it is beneficial to take the probability distribution of tolerances into account and perform a statistical analysis.
Distribution of Tolerances
In the worst-case example above there was an extreme distribution of tolerances. The question now is what a (more) realistic distribution is. That question is not that easy to answer but a better estimate would increase the accuracy of your analysis.
When similar parts have been produced already, you have important data at hand to make a good estimation of the tolerance distribution. But what if you’re working on a new product and you don’t have this kind of data for comparison at hand?
Normal Distribution of Tolerances
If you don’t know the distribution of tolerances, you have to make an estimation. Often it is assumed that tolerances have a normal (Gaussian) distribution. This is because the normal distribution seems to arise in ‘almost all cases’. In statistics this is called the central limit theorem. Roughly speaking, this theorem says that “the sum of a large number of small and independent random variables will be approximately normally distributed”. Because the production process of machined parts consists of a lot of variables, a normal distribution of tolerances is safe to assume. An additional benefit is that adding up normal distributed tolerances is relatively easy.
An assumption that is often made is that the tolerance limits coincide with the +/-3σ (3x standard deviation) values. To remind (?) you: the standard deviation is a measure for the variation. 99.7% of the population falls within the +/-3σ limits.
Statistical Stack-up Tolerance Analysis
A widely used method for performing a statistical stack-up tolerance analysis is the root-sum-squares (RSS) method. Variances (the standard deviation is the square root of variance) can be added. And that makes it easy to add up normal distributed tolerances: Ttot = √(T12 + T22 + …. Tn2).
In the example above, all tolerances where +/-1, so the total height variation becomes: Ttot = √(12 + 12 + 12 + 12) = 2. The stack of parts will have a height of 40 +/-2. And 0.3% of the stacks will be smaller or bigger (with a height of 36 .. 38 or 42 .. 44).
Tolerance Analysis Stack-up Spreadsheet
A tolerance analysis spreadsheet is available in the Engineering Toolkit of Vink System Design & Analysis. This allows you to quickly start making tolerance analyses, including the statistical method as described here. The advanced method as described in ‘Advanced Method of Tolerance Analysis‘ is also possible.
In a next article I will discuss how realistic a normal (Gaussian) distribution is.
