Up to and including HertzWin 3.2.0, all calculated results are for a static situation. The most important material stresses for a static situation are the maximum shear stress and the von Mises equivalent stress. The Von Mises equivalent stress is most often used to determine whether or not a material is overloaded. The maximum shear stress can be used for the Tresca criterion. Both criteria, Von Mises and Tresca, are usually close to each other in value and also in location: on the centerline of the contact (without tangential load), below the contact surface.
An important stress for fatigue in a rolling contact
Stress evaluation is different in a dynamic situation, such as a rolling contact in a bearing. Looking at the point where the maximum von Mises stress (or shear stress) occurs, the stress value in a rolling contact at that point in the material varies between zero and the maximum value.
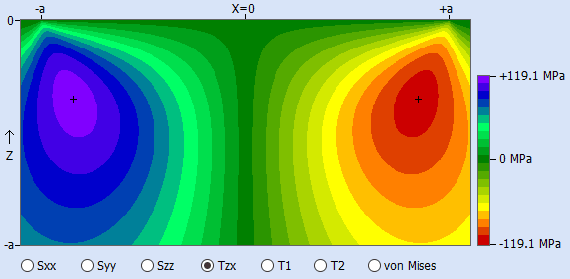
Other points in the material will experience different stress changes. An important stress for fatigue in a rolling contact is shown in the figure below. It shows the orthogonal shear stress in the X-direction in the XZ-plan (figure created with HertzWin).
Another stress considered important in fatigue life is the octahedral shear stress. However, there is disagreement as to which is the best to use. See also T.A. Harris, M.N. Kotzalas, Essential Concepts of Bearing Technology.
Stress Variation from Positive to Negative values
The maxima of the orthogonal shear stresses are located near the edge of the contact, some distance below the contact surface. The maximum value of this orthogonal shear stress is always slightly lower than the maximum shear stress on the centerline. However, it varies from a maximum positive value to a maximum negative value. For fatigue, this is a more important change in stress than between zero and maximum..
Note: The variation of the stress in the material between a negative and a positive value occurs only in the rolling direction. Thus, when the contact is rolling in the X direction, so to speak, the orthogonal shear stress Tzx varies between the negative and positive maxima. The orthogonal shear stress Tzy then varies between zero and the positive maximum on one side of the contact and between zero and the negative maximum on the other side of the contact.
Calculation of the Orthogonal Shear Stress
The value of the orthogonal shear stress depends on the shape of the contact surface: circular, elliptical or a line (rectangle). The stresses are simply calculated using the equations given in K.L. Johnson, Contact Mechanics. As of release 3.3.0, the orthogonal shear stress is calculated in HertzWin.
The octahedral shear stress τoct is easily calculated from the von Mises stress: τoct = (vonMises*√2)/3.
Two other interesting articles on rolling contact fatigue (RCF) in a rolling contact are: