Met het programma HertzWin kun je vanaf de eerste release Hertze punt- en lijncontacten berekenen. Ook de invloed van een tangentiële kracht kan berekend worden. HertzWin is online gratis downloadbaar, al vanaf maart 2009.
Geen benaderingsformule maar exacte formules
In oudere releases van HertzWin (ouder dan release 3.1.2) werd er een algemene benaderingsformule voor de invloed van een tangentiële kracht gebruikt. Vanaf release 3.2.0 (december 2020) kan in HertzWin de invloed van een tangentiële kracht ten gevolge van complete slip tussen beide lichamen uitgerekend worden. En nu niet meer met een benaderingsformule, maar met de exacte formules. Dit kan voor een circulair puntcontact en voor een lijncontact. En vanaf release 3.4.0 ook voor een elliptisch contact.. Een overzicht van de gebruikte formules voor de tangentiële kracht vind je in de helpfunctie van het programma, maar zijn veelal gebaseerd op van werk ‘Mechanics of Elastic Contacts‘ van A. Sackfield, D A Hills, D. Nowell.
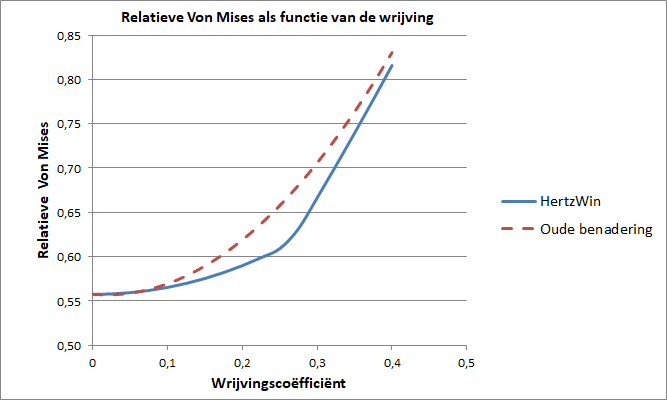
In het onderstaande figuur is de oude benadering in HertzWin uitgezet tegen de wrijvingscoëfficiënt, samen met de nieuwe, exacte methode in HertzWin. Op de verticale as staat de Von Mises (vM) vergelijkspanning ten opzichte van de maximale drukspanning (σHz): vM/σHz. De duidelijk zichtbare knik in de (blauwe) lijn is het punt waar de maximale Von Mises spanning op het oppervlak komt te liggen. De rode, onderbroken lijn is de oude benaderingsformule.
Drie situaties: wel, geen of gedeeltelijke slip
De berekening van een (Hertz) punt- of lijncontact dat belast wordt met een tangentiële kracht, wordt meestal onderverdeeld in drie verschillende situaties:
- er is geen slip tussen de beide lichamen (stick);
- er is gedeeltelijke slip tussen beide lichamen;
- beide lichamen glijden ten opzichte van elkaar.
Het eenvoudigst is de laatste situatie met volledige slip. Door wrijving veroorzaakt de slip een tangentiële kracht. Dat is de situatie die nu vanaf release 3.2 in HertzWin berekend kan worden.
Tangentiële kracht aanbrengen ná de normaalkracht
Bij het aanbrengen van een tangentiële kracht ontstaat er een koppeling (afhankelijkheid) met de normaalkracht. Bij de berekening wordt daarom uitgegaan van het volgende:
- eerst wordt de normaalkracht aangebracht. Er ontstaat een klein contactgebied dat met behulp van de gebruikelijke Hertze-theorie berekend wordt;
- daarna wordt langzaam de tangentiële kracht toegevoegd, langzaam toenemend vanaf 0 Newton;
- bij lage waarden van de tangentiële kracht (laag ten opzichte van de maximale wrijvingskracht), is er vrijwel geen slip;
- bij hogere tangentiële krachten ontstaat er aan de rand van het contact een slipzone;
- als de tangentiële kracht de maximale wrijving overschrijdt, gaat het contact over in complete slip.
Bij een normaal Hertz’ contact is de drukverdeling kwadratisch:
![]()
Met: a = halve contactbreedte, x = afstand tot het midden van het contact en σHz = maximale drukspanning in het midden van het contact.
Gaan we er van uit dat de wrijvingswet op elk punt op het contactvlak geldt, dan wordt de lokale tangentiële kracht Q(x) aan het oppervlak gegeven door de volgende functie:
![]()
Waarbijt μ de wrijvingscoëfficiënt is. Deze verdeling wordt gebruikt bij de berekening van het effect van complete slip. De volgende afbeelding laat zien hoe de krachtverdeling eruitziet als er een tangentiële kracht aanwezig is.
Berekening van een elliptisch contact
Berekeningen met een tangentiële kracht op een elliptisch contact zijn momenteel in HertzWin (nog) niet mogelijk, dat is pas voorzien in release 3.4. Het blijkt echter dat de verschillen tussen een circulair contact en een lijncontact niet erg groot zijn. zie ook de resultaten in ‘Rough Contact Between Elastically and Geometrically Identical Curved Bodies‘ van Bryant en Keer. Als het contact sterk elliptisch is kunnen de resultaten van een lijncontact met dezelfde Hertze drukspanning gebruikt worden. Is het contact bijna rond dan kunnen de resultaten voor een rond contactgebied gebruikt worden. Twee uiterste voorbeelden, beide met E-modulus 200 GPa, Poisson constante 0,3 en een wrijvingscoëfficiënt van 0,2:
- Lijncontact met radii 60 mm en 20 mm, contactlengte 100 mm, normaalkracht 5000 N. Deze situatie resulteert in een Hertze drukspanning van 341,5 MPa en een maximale Von Mises spanning van 201,5 MPa. De maximale trekspanning is 136,6 MPa;
- Puntcontact met een bol op een plat vlak, bolradius 60 mm, normaalkracht van 61,34 N. De normaalkracht is getuned zodat dit ook resulteert in een Hertze drukspanning van 341,5 MPa. De maximale Von Mises spanning is nu 217,7 MPa. De maximale trekspanning is 160,9 MPa.
Tussen dit lijncontact en het puntcontact is er een verschil van minder dan 10% voor de Von Mises en minder dan 20% voor de trekspanning. Geheel in overeenstemming met de resultaten in het artikel van Bryant en Keer. De spanningen voor een elliptisch contact zullen tussen deze resultaten in liggen. De richting van de tangentiële kracht in een elliptisch contact is evenwijdig aan de secundaire (kleine) as ‘b’. Als de tangentiële kracht evenwijdig is aan de (grote) hoofdas ‘a’, dan kunnen fouten in de afschatting groot zijn.
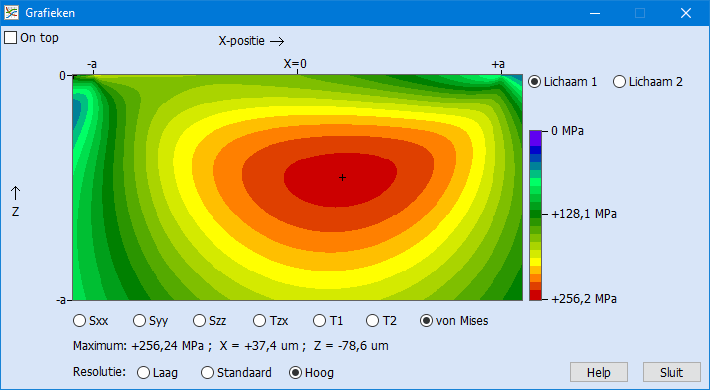
Contourplot met kleuren maken van de materiaalspanningen met HertzWin
De materiaalspanningen onder het contactvlak worden in HertzWin uitgerekend en de belangrijkste spanningen (schuifspanning, Von Mises en trekspanning) worden in het hoofdscherm weergegeven. Voor meer inzicht in de materiaalspanningen kun je contourplots maken via de grafiekenknop. Hieronder zie je een voorbeeld van zo’n contourplot voor een circulair puntcontact met een Poisson constante van 0,3 en een wrijvingscoëfficiënt van 0,2. Tip: zo’n contourplot kun je ook maken voor alleen een drukspanning als je een wrijvingscoëfficiënt van nul invuld.
Von Mises spanning verschuift naar het oppervlak bij veel wrijving en/of lage Poisson constante
Naarmate de tangentiële kracht toeneemt, verplaatst de locatie waar de maximum Von Mises spanning optreedt langzaam richting het oppervlak. In het onderstaande filmpje is het verloop te zien bij een slippend lijncontact en een toenemende wrijvingscoëfficiënt.
Belangrijk in dit voorbeeld is de constante van Poisson van 0,3. Het moment van de verschuiving richting het contactvlak hangt sterk af van de constante van Poisson. Bij een waarde lager dan ~0,2 ligt de maximale Von Mises altijd op het contactvlak.
Zoals te zien is, neemt de Von Mises spanning in het begin slechts langzaam toe: slechts +1,4% toename bij een wrijvingscoëfficiënt van 0,1 en +5,8% bij een wrijvingscoëfficiënt van 0,2. Naarmate dat de Von Mises spanning dichter bij het oppervlak komt, is de toename hoger. Dat zie je ook duidelijk in de grafiek bovenaan deze pagina. Bij een wrijvingscoëfficiënt van 0,4 is de toename van de von Mises vergelijkspanning +46,3%.