In vorige artikelen is de toepassing van statistiek in tolerantieanalyse besproken: hoe het statistisch optellen werkt, hoe je de invloed van verschillende verdelingen verwerkt en het combineren van worst-case met statistische bijdragen. Het beeld dat daaruit oprijst is dat de uitkomst van de analyse nogal kan afhangen van de aannames die je maakt. Als productdesigner weet je echter vooraf niet altijd met welke nauwkeurigheid de onderdelen geproduceerd worden. Dat maakt je analyse even goed als de aannames die je daarin doet. Als je echter werkt met de procescapabiliteitsindex Cpk dan zal dat een nauwkeurigere analyse opleveren.
Betere producten en analyses met procescapabiliteitsindex Cpk
Een mooi systeem om maatafwijkingen van onderdelen te beheersen is Six Sigma. Een belangrijk onderdeel daarin is de bepaling van de zogenaamde procescapabiliteitsindex Cpk. Onderdelen (producten) de gefabriceerd zijn met een Cpk-eis, hebben (vrijwel) altijd maatafwijkingen met een Normale (Gauss) verdeling. De procescapabiliteitsindex Cpk, populair gezegd ‘de Cpk’, is een maat voor de afstand van die Normale verdeling tot de (tolerantie) specificatie. Die Cpk kun je voor allerlei parameters in je productieproces gebruiken en leidt uiteindelijk, naast vele andere zaken, tot een (beter) beheersbaar proces. Minder uitval en ook efficiënter.
De berekening van de Cpk
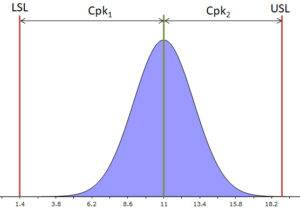
Voordat we die Cpk gaan gebruiken in de tolerantieanalyse, eerst een korte uitleg hoe de Cpk berekend wordt. Zoals gezegd, zegt de Cpk iets over de de afstand van die Normale verdeling tot de (tolerantie) specificatie. Het onderstaande figuur maakt dat duidelijk. Hierin is LSL de Lower Specification Limit en USL de Upper Specification Limit. In de praktijk zijn dit je tolerantiegrenzen. Let wel dat de Cpk de relatieve afstand is. In formulevorm is de Cpk: Cpk1 = (μ – LSL)/3σ en Cpk2 = (USL – μ)/3σ. Met μ = gemiddelde waarde (midden van de Normale verdeling) en σ de standaarddeviatie. De kleinste waarde van de twee is ‘de Cpk’.
Cpk gebruiken, heb je nu alle informatie?
Dus als je de Cpk van de onderdelen in je tolerantieanalyse weet, dan kun je dat eenvoudig gebruiken? Het antwoord is ja en nee. Ja, want je kunt aannemen dat het gemiddelde van al je maatafwijkingen allemaal precies nul zijn. Nee, omdat je hiermee weer een aanname doet. Als de Cpk bekend is, dan weet je nog niet wat de gemiddelde afwijking μ is. En die heb je nodig in je tolerantieanalyse.
Je kunt nu twee dingen doen:
- Vooraf specificeren wat de maximale afwijking van het gemiddelde μ mag zijn.
- Een aanname doen ten aanzien van de maximale afwijking van het gemiddelde μ.
Het is duidelijk dat 1) de voorkeur heeft. Dan weet je namelijk precies wat de mogelijke afwijkingen zijn. Als 1) niet kan, dan zul je een aanname moeten maken. Dat is niet erg, heel erg veel (productie) bedrijven doen dat. Een veel gebruikte methode is het eerder genoemde Six Sigma.
Six Sigma-methode, een kort overzicht
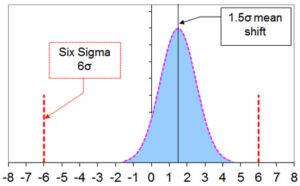
De Six Sigma-methode is in 1986 door Motorola ontwikkeld op basis van observaties in hun productie. Daarin zagen zij dat, ook in goed beheerste processen, de gemiddelden μ enige drift vertoonden. En de maximale drift is door Motorola gekwantificeerd als +/-1.5σ. Het klinkt misschien gek dat de verschuiving van het gemiddelde een factor van de standaarddeviatie σ is. Maar als je wat langer nadenkt dan is het eigenlijk wel logisch. Het zou vreemd zijn als je een heel nauwkeurig proces hebt, een kleine σ, met een grote drift. En andersom ook. De naam van de methode is ontleend aan de specificatielimieten: +/-6σ. De onderstaande figuur beeld dat uit. Een proces dat aan Six Sigma voldoet, kent een Cpk van 1.5 (=(6σ-1.5σ)/3σ).
Interessant is verder dat de maximaal te verwachten uitval 3.4 ppm (3.4 x 10-6) is. Je moet hier bij bedenken dat door de drift alleen éénzijdige overschrijdingen van de 6σ-grens een rol spelen. En verder dat de afstand van het gemiddelde tot de 6σ-grens slechts 4.5σ is. Als je dit even wilt narekenen in MS Excel, dan kun je deze formule gebruiken:
=NORM.DIST(-4.5,0,1,TRUE) óf =1-NORM.DIST(4.5,0,1,TRUE).
Cpk in je tolerantieanalyse gebruiken
Dus als de (toegestane) gemiddelde afwijking μ niet bekend is, kun je net als heel veel andere bedrijven de waarden μ=1.5σ gebruiken. Laten we dat invullen in de formule voor de Cpk en verder stellen dat de LSL en de USL gelijk zijn aan je (symmetrische!) tolerantie ‘Tol’. Dan krijg je na omwerken: σ = Tol / (1.5 + 3Cpk). Wil je de factor 1.5 niet gebruiken maar de factor k (μ=kσ) dan krijg je: σ = Tol / (k + 3Cpk). Omdat je vrijwel altijd rekent met 3σ, moet je dit antwoord nog met 3 vermenigvuldigen.
Je krijgt nu twee kolommen per vrijheidsgraad in je tolerantietabel. Eentje met de 3σ-waarde en eentje met de te verwachten maximale drift μ. De 3σ-waarden kun je eenvoudig statistisch optellen, maar hoe tel je nu die afzonderlijke driftwaarden op?
Drift verwerken in je tolerantietabel. Verwerk het in een template!
Drift is vaak geen verschijnsel dat makkelijk uitmiddelt. Dus statistisch optellen ligt niet voor de hand. Aan de andere kant is worst-case optellen wel weer erg pessimistisch. Het is vast niet zo dat de drift altijd voor alle onderdelen in je tolerantieketen altijd maximaal ongunstig uitpakt. Dus iets er tussen in? Ja, iets er tussen in lijkt het beste. Ik ben een groot voorstander van de aanname dat de drift μ random verdeeld is voor elk onderdeel in je tolerantieketen. Niet té optimistisch door statistisch op te tellen en ook niet té pessimistisch door de drift als worst-case te beschouwen
Random verdeeld is hetzelfde als uniform verdeeld. En uniform verdeelde waarden mag je statistisch optellen mét een correctiefactor. Voor uniform verdeelde waarden is de correctiefactor precies √3. Het is niet nodig om dat zelf allemaal uit te werken. Al dit denk- en rekenwerk is standaard aanwezig in het template TolStackUp, hier verkrijgbaar op de site.