Uitwerking tolerantieanalyse met TolStackUp van een constructie

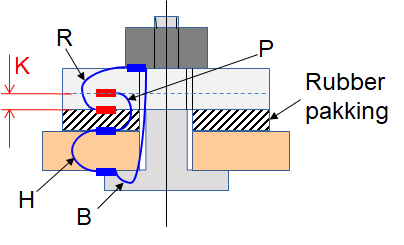
In het artikel ‘Het opstellen van de tolerantieketen in stappen‘, is aan de hand van een voorbeeld beschreven hoe je in stappen een tolerantieketen opstelt. Het artikel eindigde met een schets van de keten. Die zie je in het hier in het onderstaande figuur. Door nu de maten en toleranties van de 4 onderdelen te verwerken met (bijvoorbeeld) TolStackUp, geeft je een complete tolerantieanalyse.

Tolerantieketen uitwerken met afmetingen en toleranties

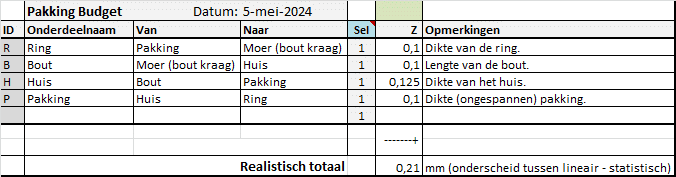
Laten we dit voorbeeld eens met getallen uitwerken en invullen in het TolStackUp spreadsheet. Dan is de tolerantieanalyse compleet. Ik neem de volgende (arbitraire) waarden aan:

• P = 4 +/-0,1
• R = 8 +0,2/0
• B = 21 +/-0,1
• H = 10 +0,1/-0,15

Als je deze gegevens en de benamingen invult in de tolerantiepool (kolommen H, I, J), dan ziet dat er uit als in onderstaande figuur. Merk op dat de tolerantie van het ‘Huis’ afgerond wordt weergegeven, maar de werkelijke waarde van +/-0,125 mm wordt gebruikt in de berekeningen.

Invullen van de toleranties in de tabel

Het enige dat je nu nog moet doen is de 4 codes (P, R, B, H) invullen in kolom B van de tolerantietabel (blad ‘Tolerance Chain’). De gegevens van de tolerantiepool en de totaalsom verschijnen direct. Voor de duidelijkheid heb ik een aantal (meestal lege) rijen en kolommen verwijderd:

Om te kunnen beoordelen of de gekozen toleranties voldoen, moet je de specificaties opstellen en invullen. Om het voorbeeld verder te kunnen invullen stel ik de volgende specificatie:

• Minimale indrukking voor een goede afsluiting is 0,8 mm;
• Om beschadiging van de pakking te voorkomen is de maximale indrukking 1,3 mm.

Hoe vul je de specificatie in?

Daarvoor kijk je eerst naar de nominale indrukking. Die nominale indrukking kun je zien als je de kolommen F t/m Q uitklapt. Hieronder zie je een kleine uitsnede. Let ook op hoe je de ‘richting’ van de absolute maat (handmatig) aangeeft in kolom J.

Je ziet nu dat de nominale indrukking op 1,075 mm ligt. Misschien had je precies 1 mm verwacht, maar door de asymmetrische tolerantie van de Ring en het Huis is de verwachtte indrukking dus ietsje hoger. De indrukking van de pakking is op basis van deze analyse dus: 1,075 +/- 0,21 mm.

Nu kunnen we de specificatie bepalen en invullen in het spreadsheet:

• Eis voor minimale indrukking: 0,8 mm – 1,075 mm = -0,275 mm.
• Eis voor maximale indrukking: 1,3 mm – 1,075 mm = 0,225 mm.

Vul je deze twee specificaties in, dan zie je het totaalbeeld.

Welke conclusies kun je trekken?

De volgende conclusies kunnen worden getrokken:

• De vier toleranties voldoen samen nét. De capability (1.05) geeft aan dat er slechts 5% marge is ten opzichte van de specificatie.
• Het geschatte uitvalpercentage is 0,08%.
• De ondergrens en de bovengrens van de specificaties zijn ongelijk. Dit betekent dat de nominale maten van de onderdelen niet optimaal gekozen zijn.

Let op dat de bovenstaande analyse en conclusies zijn gebaseerd op de aanname dat de toleranties Normaal verdeeld zijn en dat de 3σ-waarden precies gelijk zijn aan de tolerantie-eisen op tekening. Die aanname zal in de praktijk nooit helemaal kloppen.

Welke verbeteringen zijn door te voeren?

Er is (te) weinig marge tussen de te verwachtte variatie en de specificatie. Vooral omdat niet duidelijk is of de hier boven genoemde aanname wel correct is. Eén verbetering is vrij eenvoudig door te voeren: de nominale indrukking van de pakking aanpassen zodat deze precies midden tussen de twee specificatiegrenzen ligt. De nominale indrukking moet dan zijn: (0,8 mm + 1,3 mm)/2 = 1,05 mm.

Het maakt niet uit welk onderdeel je aanpast. Ik neem als voorbeeld het ‘Huis’ dat dan een dikte krijgt van 9,975 -0,15/+0,1 mm. Analyse leert dat de capability dan stijgt naar 1,17 en het uitvalpercentage halveert.

De tweede verbetering zou kunnen zijn het verkleinen van één of meerdere toleranties. Ook dat is vrij eenvoudig te doen. Maar een andere mogelijkheid is om de onderdelen te produceren via een nauwkeurig gecontroleerd proces, een SPC-proces. Zo’n SPC-proces is vooral heel geschikt voor massafabricage. Laten we eens zien wat dat voor dit voorbeeld aan winst oplevert.

SPC-tolerantieanalyse

SPC-tolerantieanalyse verschilt met de standaard analyse in die zin dat er bij SPC-tolerantieanalyse van uit wordt gegaan dat de onderdelen in de constructie geproduceerd worden met ‘SPC-eisen’. Een SPC-tolerantieanalyse is dus niet heel veel anders dan een standaard analyse. Het enige dat je hoeft te doen is precies dezelfde getallen in te vullen in het blad ‘SPC-TolerancePool’ van TolStackUp. En de codes in te vullen in de/een tabel in het blad ‘SPC Tolerance Chain’.

Hieronder zie je de resultaten, eerst de SPC-TolerancePool en daaronder de bijbehorende tolerantietabel. De enige aanpassing die gedaan is, is de nominale waarde van het ‘Huis’. Die is van 10 mm gewijzigd in 9,975 mm, de verbetering die hier boven is aangegeven. De standaard ingestelde eis van Cpk = 1,5 en de maximaal toegestane afwijking van het gemiddelde μ = 1,5σ is ongewijzigd. Deze zijn gelijk aan de 6-sigma eisen.

Nu zie je drie dingen:

• De specificaties van de onder- en bovengrens zijn gelijk. De nominale maat ligt dus precies goed binnen de gestelde eisen.
• De Cpk = 1,47 en kleurt rood. De rode kleur is omdat het TolStackUp spreadsheet automatisch dezelfde eis aan de uitkomst stelt als de eis aan de samenstellende onderdelen. Dit is natuurlijk naar eigen wensen aan te passen.
• Het geschatte uitvalpercentage is gedaald van 0,08% naar 0,0005%. 16 keer lager!

Deze uitkomst is beter (minder uitval) maar ook betrouwbaarder. De hogere betrouwbaarheid van de uitkomst komt door de Cpk eisen aan de onderdelen.

Conclusie

Heb je eenmaal een tolerantieketen opgesteld, dan is een tolerantieanalyse met TolStackUp snel gemaakt. De uitkomst van de analyse geeft je dan al direct inzicht in de constructie en wat er eventueel verbeterd kan worden. Het toepassen van SPC resulteert in een veel grotere betrouwbaarheid van zowel de productie als je tolerantieanalyse.