Het gatscharnier is een met succes toegepast constructie-element in fijnmechanische systemen. Het ontstaat door het boren of vonkeroderen van twee naast elkaar liggende gaten.
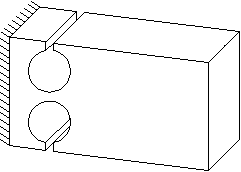
Tegenover positieve eigenschappen (spelingsvrij, wrijvingsloos) van gatscharnieren, staat de beperkte hoekverdraaiing. Om een gatscharnier goed te kunnen dimensioneren moet er een optimum gezocht worden tussen de gewenste hoekverdraaiing, stijfheid en maximale materiaalspanning. Het vergt meestal enig rekenwerk voordat een voldoende goede dimensionering is gevonden. Er zijn hiervoor verschillende formules in omloop. Die zijn gebaseerd op het theoretisch oplossen van de krachtsvergelijkingen of gebaseerd op benaderingen van eindige elementen analyse (FEM).
Theoretische afleiding van de stijfheid
Het berekenen van de stijfheid van een gatscharnier en de optredende materiaalspanning onder belasting, is geen eenvoudige zaak. In de loop der jaren zijn er heel wat artikelen verschenen over het oplossen van de krachtsvergelijkingen voor het gatscharnier. Het artikel van J.M Paros en L. Weisbord (‘How to design flexure hinges’, Machine Design 25 november 1965) is een van de bekendste. Ook N. Lobontiu, Wu en Zhou, en Tseytlin hebben formules afgeleid voor het berekenen van gatscharnieren.
Een beperking van deze theoretische benaderingen is dat het gatscharnier geïsoleerd beschouwd wordt. En vervormingen van het basismateriaal naast het versmalde deel van het gatscharnier niet meegenomen worden. Voor de constructeur betekent dit dat in de praktijk de stijfheid van het gatscharnier lager zal zijn.
Praktische benadering met FEM-gebaseerde formules
Voor praktische toepassingen kan een nauwkeurige bepaling van de gatscharnierstijfheid belangrijk zijn. In het collegedictaat “Het voorspellen van dynamisch gedrag en positioneernauwkeurigheid van constructies en mechanismen, W. van der Hoek 1981” zijn empirische formules (gebaseerd op FEM) gegeven voor het bepalen van de stijfheden en optredende materiaalspanningen. In een artikel van Y.K. Yong (Review of circular flexure hinge design equations and derivation of empirical formulations, 2007) worden verschillende theoretische en empirische benaderingen met elkaar vergeleken. In zijn artikel refereert hij aan een artikel van W.O. Schotborgh et all. waarin de empirische formules van W. van der Hoek gebruikt worden. De conclusie van Yong is dat deze empirische formules de hoogste nauwkeurigheid geven, met fouten <2.5%. Omdat deze formules ook nog eens makkelijk toe te passen zijn, zijn ze erg geschikt voor de praktijk van de constructeur.
Het gratis programma FlexHinge, dat is ontwikkeld door Vink System Design & Analysis en dat u van deze website kunt downloaden, gebruikt deze empirische formules.