In een vorig artikel is het hele stappenplan voor het opstellen van de tolerantieketen beschreven. Het is beschreven aan de hand van een relatief eenvoudig voorbeeld. In de praktijk kunnen de constructies echter heel wat complexer zijn. En dan is de tolerantieanalyse van zo’n constructie ook heel wat ingewikkelder. Maar ook voor een relatief eenvoudige constructie kan de tolerantieanalyse lastig zijn. Daarom nu een eenvoudig klemmechanisme om het proces van tolerantieanalyse en het stappenplan verder te verduidelijken.
Het opstellen van een tolerantieketen stuit soms op constructie-elementen die op het eerste gezicht lastig zijn op te nemen. Vaker voorkomende elementen zijn bijvoorbeeld: veren, hefbomen en speling. Daarom nu een voorbeeld waar twee van deze elementen in voorkomen.
Een eenvoudig ontwerp, maar een lastige tolerantieanalyse
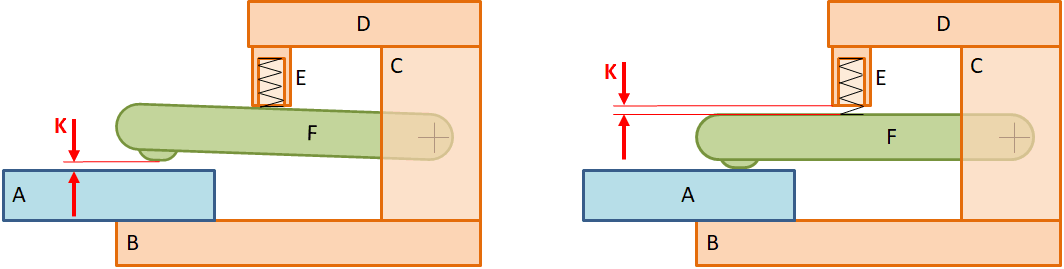
De constructie is een klemmechanisme die in een geautomatiseerd productieproces platen moet vastklemmen voor een bewerking. De klemkracht wordt door een veer uitgeoefend. Na de bewerking zorgt een tegenkracht dat de klem open gaat. De plaat ‘verlaat’ de kleminrichting en een nieuwe plaat schuift in de klem. De volgende twee figuren laten een eenvoudige schets van de constructie zien. Er is een veer aanwezig (in onderdeel E), een hefboom (onderdeel F) en een speling. De speling is niet zichtbaar in de figuur maar zit in het draaipunt van de hefboom F in kolom C. Tussen open- en dichtgaan van de klem wordt de hele speling doorlopen.
Let op: deze schets is eigenlijk al stap 3 in het stappenplan zoals beschreven in Het opstellen van de tolerantieketen in stappen.
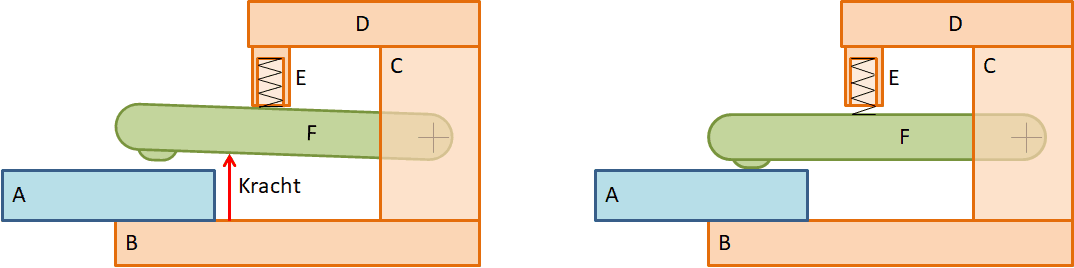
Klemmechanisme met hefboom open en dicht.
Wat kan er mis gaan, de kritische maat
Het is hier niet de vraag of dit de meest optimale constructie is. Er kunnen allerlei redenen zijn om tot dit ontwerp te komen. Het gaat nu om de tolerantieanalyse voor deze constructie. De eerste stap, stap 1, is het bepalen van de kritische maat. Om die kritische maat te bepalen is het meestal handig om de vraag te stellen: wat kan er mis gaan?
Zoals je in de twee figuren ziet, kan de klem maar een klein stukje open. Een probleem dat zich voor zou kunnen doen is dat de plaat A niet in de klem past als die open staat. Dus door een combinatie van een ’te dikke’ plaat A en andere ongunstig uitvallende toleranties. De kritische maat zal dus te maken hebben met de opening van de klem. Maar laten we eerst naar de machinetoestanden kijken voordat we de kritische maat definitief bepalen.
Machinetoestanden
Stap 2 van het stappenplan gaat over machinetoestanden. In dit ontwerp van het klemmechanisme zijn dat er twee: open en dicht. Het zal duidelijk zijn dat de toestand ‘dicht’ niet van belang is voor het geschetste probleem. Als de klem dicht is, dan zit er al een plaat in de klem en is er geen probleem. Het gaat dus om de toestand open.
Welke kritische maat te kiezen?
Het lijkt nu voor de hand te liggen om de kritische maat in de schets te tekenen in de toestand ‘open’. Dit is het meest logische omdat dit de toestand aan geeft waarbij het probleem van een niet passende plaat kan optreden. Maar het is ook mogelijk om de kritische maat in de toestand ‘dicht’ te definiëren. Onderstaande figuren laten beide zien. Welke je kiest maakt in de praktijk niet uit. In de tolerantieketen zitten uiteindelijk precies dezelfde toleranties. En dus zijn de einduitkomsten (capability en uitvalpercentage) precies gelijk aan elkaar.
Kritische maat K voor toestand ‘open’ en voor toestand ‘dicht’.
Welke van de twee je kiest is voor de einduitkomst dus niet zo belangrijk. Maar om je tolerantieanalyse uit te leggen aan iemand anders, bijvoorbeeld in een review, is het handig om die van de toestand ‘open’ uit te leggen. Maar soms is het uitwerken van de tolerantieketen van de andere toestand (voor jou) makkelijker. We kiezen hier voor de kritische maat in de toestand ‘open’.
De tolerantieketen
We zijn nu aangeland in stap 4 van het stappenplan. Hoe de tolerantieketen er nu uitziet, is een kwestie van puzzelen. Het gaat er om, om alle invloeden op de kritische maat in de keten op te nemen. Een belangrijke stap hierin is, is om de interfaces van de onderdelen te bepalen die voor zullen komen in de keten. Elk onderdeel in de tolerantieketen heeft altijd twee interfaces. En de tolerantieketen gaat door deze twee interfaces heen. Maar hoe weet je nu vooraf welke interfaces je nodig hebt als je de keten nog niet kent?
Strategieën
Als de keten je niet direct duidelijk is, kun je verschillende strategieën gebruiken om de tolerantieketen te bepalen:
- Begin aan één kant van de kritische maat en zoek een weg door de constructie naar de andere kant van de kritische maat. Als je vastloopt dan ga je verder aan de andere kant van de kritische maat en kijk je of je vanaf die kant ‘contact’ kunt maken met het punt waar je gebleven was;
- Kom je nu weer niet verder, dan kun je een of meerdere ‘gedachte-experimenten‘ doen. Neem een onderdeel van de constructie in gedachten en laat een maat waarvan je vermoed dat deze in de keten zit, in grootte variëren. Bedenk nu of dat invloed heeft op de kritische maat. Zo ja, dan moet dit onderdeel met deze maat in de tolerantieketen opgenomen worden. Voorbeeld: de hoogte van blok C. Als je die hoogte in gedachten laat toe- of afnemen, dan zie je dat dat invloed heeft op de kritische maat. Die doet dus mee in de keten. De tolerantieketen moet door dit onderdeel heen. Als de constructie erg ingewikkeld is, kun je dit natuurlijk ook in je CAD-tekening doen.
- Als de constructie erg complex is, kun je ook een sterk versimpelde schets maken. In die schets vat je enkele onderdelen steeds samen in één lijn van de keten, groeperen dus. Dan krijg je een globale keten. En als je die globale keten eenmaal klaar hebt, een keten die gesloten is, dan ga je in detail de gegroepeerde lijnen uitwerken.
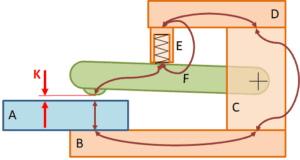
Als we dit nu doen voor het klemmechanisme, dan kunnen we uitkomen op de tolerantieketen zoals in onderstaande figuur.
Eerste deel van de tolerantieketen
Kort samengevat zijn de elementen die de kritische maat beïnvloeden: de hoogte/dikte maten van onderdelen A, C, E en F + de vlakheid/rechtheid van onderdelen B en D + de speling.
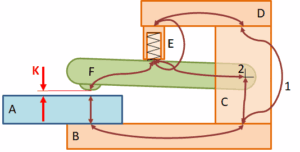
Maar we zijn nog niet klaar. De positie van het scharnierpunt van de hefboom heeft ook invloed op de kritische maat. Gek genoeg krijg je nu dus twee routes door de constructie, zie onderstaande figuur. De twee routes zijn aangegeven met een 1 en het toegevoegde stukje 2.
Complete tolerantieketen voor toestand ‘open’.
Kan dat eigenlijk wel? Ja, het gaat niet om de tekening van de tolerantieketen maar om alle invloeden op de kritische maat te verzamelen. De schets met de tolerantieketen is slechts een hulpmiddel om dat doel te bereiken.
Interfaces, maten en toleranties
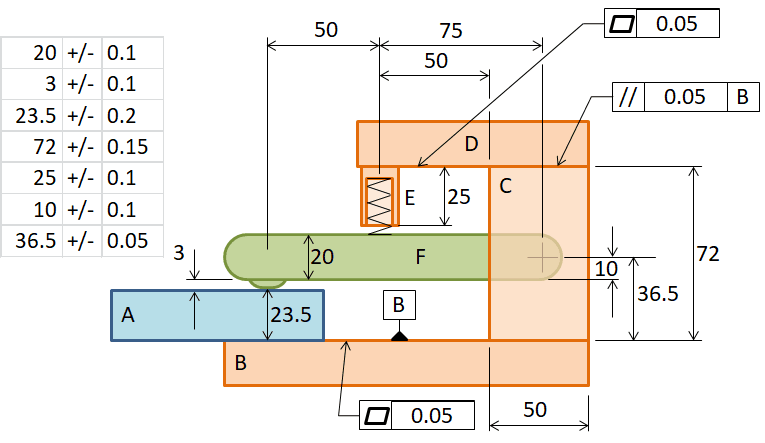
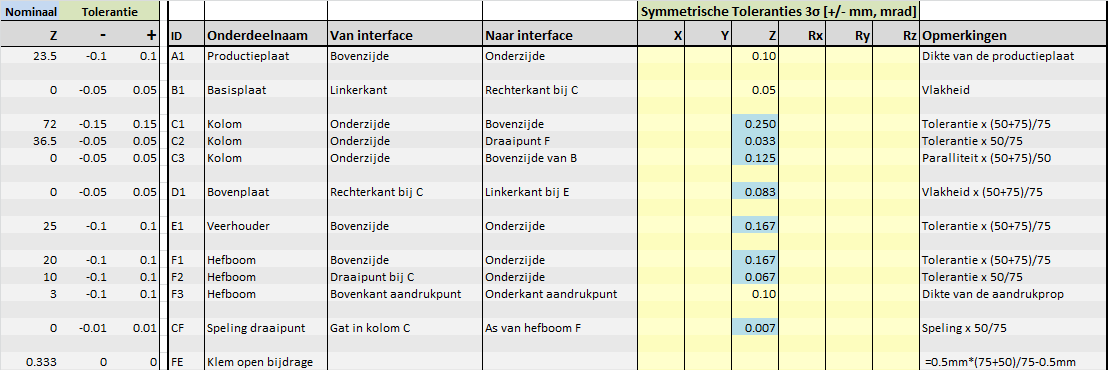
Nu de tolerantieketen bekend is, kun je aan de hand daarvan alle maten en toleranties verzamelen. Dat is meestal niet zo moeilijk. Als het een al bestaande constructie is, kun je ze opzoeken. En als de constructie alleen nog maar als concept bestaat, kun je de maten en toleranties zelf bepalen. Deze laatste situatie is ideaal en zoals het zou moeten zijn: je kunt aan de hand van de tolerantietabel de best passende toleranties bepalen! Hieronder in de figuur zie je alle maten en toleranties die meedoen. Ik heb in dit voorbeeld gekozen voor symmetrische toleranties, maar in het TolStackUp-template kun je ook asymmetrische toleranties opnemen. Die asymmetrische toleranties worden dan automatisch correct verwerkt.
De speling staat niet in de figuur, die is aangegeven als +/-0.01 mm. Verder zie je dat in bovenstaande schets voor de hefboom slechts twee pijlen staan, eentje vanaf het draaipunt en eentje naar het aandrukpunt voor de productieplaat. Deze laatste bestaat volgens de onderstaande maatschets eigenlijk uit twee maten en toleranties. Voor de duidelijkheid van de figuur zijn die twee dus samengevat in één pijl. Maar in de tolerantietabel zijn dit dus twee bijdragen!
Alle relevante maten van het klemmechanisme.
Tolerantietabel vullen
De meeste maten en toleranties kun je eenvoudig in de tolerantietabel zetten. Het TolStackUp tolerantie spreadsheet is hier uitstekend voor geschikt. De moeilijkheid van deze stap is echter hoe je precies alle relevante toleranties vertaalt naar waarden in de tolerantietabel. Behalve effecten van de hefboom gaat het ook om het effect van de vlakheid van onderdelen B en D, en het effect van de parallelliteit van onderdeel C (0.05 t.o.v. B).
Laten we eens kijken naar de hoogtemaat (20 mm) van onderdeel E, die een tolerantie van +/-0.1 mm heeft. Deze tolerantie werkt via de hefboom (onderdeel F) versterkt door in de kritische maat K. Die versterkingsfactor is: (50 mm + 75 mm)/(75 mm) = 1.67 (1 2/3). Dus de bijdrage van de tolerantie van onderdeel E is +/-0.1 mm x 1.67 = +/-0.167 mm.
Op soortgelijke wijze worden hier alle bijdragen beschreven. We beginnen bij de kritische maat K, onderdeel A en lopen dan de hele keten langs. Je zult zien dat vrij veel toleranties door een hefboomeffect versterkt of verzwakt worden!
De basisgedachte bij het bepalen van een individuele bijdrage is om alléén die ene tolerantie (in gedachten) te laten variëren, terwijl je alle andere maten op hun nominale waarde ‘vasthoudt’. In andere woorden: in gedachten (of CAD) is alles perfect (tot op de micrometer) gemaakt. En alleen de maat waarvan je de tolerantiebijdrage wilt bepalen varieert in grootte. Zie wat er dan gebeurt met de kritische maat.
De individuele bijdragen
- De productieplaat A heeft een eenvoudige bijdrage. Nominale maat 23.5 mm met tolerantie +/-0.1 mm.
- De basisplaat B voegt een vlakheidstolerantie toe. In het onderstaande figuur staan twee mogelijke worst-case gevallen.

De vlakheid is gespecificeerd op 0.05 mm, dat zich vertaalt naar +/-0.05 mm in de tolerantietabel. Door deze variatie ontstaat er een hoogtevariatie van het aanslagpunt bij veerhouder E maar ook het draaipunt van de hefboom beweegt mee. Dus de vlakheidstolerantie werkt één op één door in de kritische maat K. - De kolom C voegt drie toleranties toe: de hoogtemaat 72 +/- 0.15 mm, de parallelliteit 0.05 mm en de positie van het draaipunt 36.5 +/- 0.05 mm. Door de hefboom is het effect op de kritische maat voor elke tolerantie verschillend:
– Hoogtemaat 72 +/- 0.15 mm. Ten gevolge van deze hoogtevariatie is er een hoogtevariatie van het aanslagpunt bij veerhouder E van +/- 0.15 mm. Door de hefboomwerking is het effect op de kritische maat: +/- 0.15 mm x (50+75)/75 = +/-0.25 mm;
– Parallelliteit 0.05 mm. Hierdoor zal er een hoogtevariatie van het aanslagpunt bij veerhouder E optreden. De hefboom volgt het aanslagpunt bij E en de opening voor de productieplaat A (de kritische maat) wordt daarmee groter of kleiner. Het effect is: +/-0.05 mm x (50+75)/50 = +/-0.125 mm;
– Positie draaipunt 36.5 +/- 0.05 mm. Verschuiving van het draaipunt resulteert in een variatie in de kritische maat K. Door de hefboomarmen van 75 mm en 50 mm, is het een verzwakkend effect: +/-0.05 mm x 50/75 = +/-0.033 mm. - De bovenplaat D voegt een vlakheidstolerantie toe. Ook nu wordt +/-0.05 mm in de tolerantietabel opgenomen. Maar het draaipunt ‘beweegt’ nu niet mee. Alleen het aanslagpunt bij E verplaatst mee met deze vlakheidstolerantie. Door de hefboom is het effect: +/-0.05 mm x (50+75)/75 = +/-0.083 mm.
- Veerhouder E 25 +/-0.1 mm. Door de hefboom is het effect: +/-0.1 mm x (50+75)/75 = +/-0.167 mm.
- De hefboom F voegt drie bijdragen toe aan de tolerantietabel: de dikte van 20 +/-0.1 mm, de dikte van het aandrukpunt 3 +/-0.1 mm en de positie van het draaipunt 10 +/-0.1 mm. De invloed op de kritische maat is echter steeds anders:
– Diktemaat 20 +/-0.1 mm. Deze bijdrage is wat lastiger te doorzien. Belangrijk hier is om te kijken naar de maatlijn voor de positie van het draaipunt. Deze staat naar de ‘onderkant’ van de hefboom. Als de positie van het draaipunt in de hefboom niet varieert, dan werkt de diktevariatie (20 +/-0.1 mm) van de hefboom aan de bovenkant door. Door de hefboomwerking is de bijdrage nu +/-0.1 mm x (50+75)/75 = +/-0.167 mm.
– Aandrukpunt 3 +/-0.1 mm. Het aandrukpunt heeft een eenvoudige bijdrage. Nominale maat 3 mm met tolerantie +/-0.1;
– Draaipunt 10 +/-0.1 mm. De invloed is analoog aan die van het draaipunt in kolom C: +/-0.1 mm x 50/75 = +/-0.067 mm. - De speling van het draaipunt +/-0.01. Hoe speling precies uitpakt, kan soms lastig te bepalen zijn. Om daar niet lang over uit te weiden in dit artikel ga ik voor de eenvoud uit van de gemiddelde speling +/-0.01 mm. Het is wel goed om te beseffen dat de aanwezige speling altijd helemaal doorlopen wordt tussen de twee toestanden open en dicht. Door de hefboomwerking is de bijdrage beperkt: +/-0.01 mm x 50/75 = +/-0.007 mm. Een kleine onnauwkeurigheid in de bijdrage is dus niet zo erg.
De nominale kritische maat bepalen
In veel tolerantieanalyses kun je eenvoudig de nominale maten optellen (met het juiste plus- en minteken). Het resultaat is dan de nominale kritische maat. In dit voorbeeld speelt er echter nog iets bijzonders mee. Als je de nominale maten van het klemmechanisme optelt, dan is het resultaat de nominale afstand tussen de hefboom F en de veerhouder E in gesloten toestand! Om de nominale kritische maat in de open toestand te krijgen, moet je nog vermenigvuldigen met een ‘hefboomfactor‘. Die factor is eenvoudig te bepalen met de gegeven armlengten: (50+75)/75 = 1.67. In de tolerantietabel neem ik alleen het verschil mee tussen de afstand bij E en de afstand bij de plaat A: 0.5mm*(75+50)/75-0.5mm = 0.333 mm.
Invullen van de bijdragen in TolStackUp
Al deze maten en toleranties vullen we in de tolerantiepool van TolStackUp in. De tolerantiepool in TolStackUp is een centrale sheet waar alle toleranties via een verwijzing ‘vandaan gehaald’ worden. Zo kun je een en dezelfde tolerantie in meerdere ketens gebruiken zonder ingewikkelde administratie. Onderstaande figuur geeft het resultaat. Ik heb voor de duidelijkheid enkele overbodige kolommen verborgen. Aan de linkerkant zie je drie kolommen waar de maten en toleranties staan zoals ze op tekening zijn aangegeven. Daarnaast zie je een code (A, B1, etc.), de naam van het onderdeel en de interfaces. De geel gekleurde kolommen worden automatisch uitgerekend en in de rechterkolom kun je nog opmerkingen kwijt. Alle grijs gekleurde kolommen zijn vrij in te vullen.
Ingevulde tolerantietabel in TolStackUp.
Van alle bijdragen die niet één op één doorwerken maar via een hefboom, heb ik de formule aangepast en het vakje donkerder gekleurd. Een andere methode die ik hier ook had kunnen gebruiken is de mogelijkheid in TolStackUp om vectoren te definiëren. Die vectoren zijn dan de verschillende versterking- of verzwakkingsfactoren van de hefboom. Die definitie komt in de ‘vectorpool‘ en die kun je dan gebruiken in de 6DOF tolerantietabel. Een beschrijving daarvan doe ik in een volgend artikel.
Ingevulde tolerantieketen
In de tolerantiepool is voor elke tolerantie een unieke code ingevuld. Dat maakt het invullen van de uiteindelijke tolerantieketen erg eenvoudig in TolStackUp. Vul voor elke bijdrage in de keten de bijbehorende code in (in de eerste kolom) en de hele keten wordt automatisch gevuld.
Je moet nu alleen nog de twee smalle, grijs gekleurde kolommen bekijken en eventueel aanpassen:
- Voor de optelling van de nominale maten kun je links van de nominale maat aangeven of deze in de positieve richting (+1) of in de negatieve richting (-1) moet meetellen. De totaalsom geeft de nominale opening aan van het klemmechanisme.
De twee maten van het draaipunt tellen niet mee. Die heb ik op 0 gezet. De keuze voor de waarde 0 is voorzien in release 2.2.0 van TolStackUp, in eerdere releases kun je de waarde in de betreffende cel verwijderen. - In de kolom ‘sel’ tussen de nominale maat en de tolerantie, kun je kiezen voor de wijze van optellen. De keuzes zijn statistisch (Normaal, random of elliptisch verdeeld) of worst-case, zie onderstaande figuur.
Mogelijke optelmethoden in TolStackUp.
Welke wijze van optellen van toleranties
Ik heb de volgende keuzes gemaakt:
- Standaard ga ik uit van Normaal verdeelde afwijkingen van de nominale maat. Dat is het meest waarschijnlijk voor beheerste productieprocessen. Er zijn misschien maar één of enkele klemmechanismen gemaakt voor de fabriek. Maar hopelijk wel in een beheerst proces en daarmee is een Normale verdeling aannemelijk;
- Voor de bijdrage van de tolerantie van de productieplaat heb ik gekozen voor een worst-case bijdrage (waarde 0 in de kolom). Het is aannemelijk dat in geautomatiseerde productieprocessen de afwijkingen van de plaatdikte Normaal verdeeld zullen zijn. Maar er gaat niet slechts één plaat geklemd worden maar heel veel platen. De kans dat die maximaal dikke plaat (platen) een keer geklemd moet worden is dus heel erg groot. En ook die plaat moet passen in de klem;
- De speling in het draaipunt heb ik als random verdeeld (uniform) aangegeven (waarde 3 in de kolom). Dat is enigszins arbitrair en je kunt compleet uitwerken hoe de speling in dit klemmechanisme doorwerkt. Dat heb ik niet gedaan, omdat de bijdrage in de optelling hooguit slechts enkele micrometers verschil geeft. Dat is iets om in een volgend artikel uit te diepen.
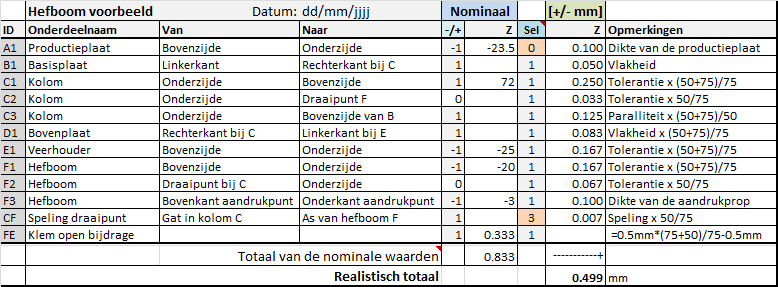
De tolerantieketen in TolStackUp geeft nu het volgende resultaat:
Uitgewerkte tolerantietabel met resultaat in TolStackUp.
Je ziet direct het resultaat: de nominale opening K is 0.833 mm en er is een maximale variatie te verwachten van +/-0.499 mm (~3σ).
Beoordeling van de tolerantieketen
Het enige dat nu nog resteert is het beoordelen van de uitkomst. In TolStackUp hoef je alleen maar de specificatie op de kritische maat in te vullen en er rolt automatisch uit hoe goed de tolerantieketen presteert, de capability, en een schatting van het uitvalpercentage.
De specificatie
Het definiëren van de specificatie kan soms lastig zijn, maar in dit uitgewerkte voorbeeld gelukkig niet. De productieplaat past wel of hij past niet. Zoals je al in de opgetelde nominale kritische maat ziet, is de opening van het klemmechanisme ontworpen op 0.833 mm. Die nominale opening kan volgens de gemaakte analyse variëren met +/-0.499 mm. Je kunt nu concluderen dat de dikste productieplaat, de plaat die helemaal aan de rand van z’n specificatie zit, nog makkelijk zal passen. De specificatie ondergrens is dus -0.833 mm. De bovengrens is onbelangrijk als een (veel) te grote opening geen probleem is. De bovengrens kun je dus op een willekeurige hoge waarde zetten. Ik heb gekozen voor +10 mm.
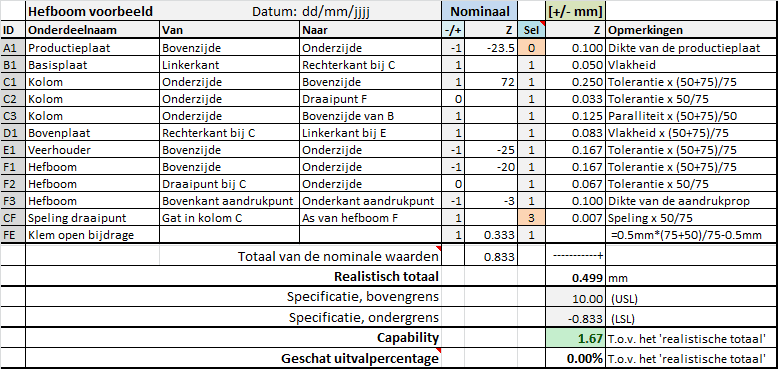
Vul je die twee specificaties in, dan krijg je het totale plaatje te zien, zie onderstaande figuur.
Uitgewerkte tolerantietabel in TolStackUp met capability en uitvalpercentage.
Zoals je al verwachtte op basis van de optelling van +/-0.499 mm, is er een behoorlijke marge ten opzichte van de specificatie. De verwachting is nu dat een productieplaat met de grootste dikte-afwijking, de dikst mogelijke plaat, er een heel kleine kans bestaat dat die niet past. De geschatte kans daarop is afgerond 0.00% (0.00000169%).
Capability en uitvalpercentage
De capability is een een getal die de ‘relatieve prestatie’ van de keten weergeeft ten opzichte van de specificatie. In formulevorm is het eenvoudig: capability = specificatie/variatie. In dit geval is dat dus 0.833/0.499 ≈ 1.67. Een waarde groter dan 1 is goed, lager dan 1 is dus niet goed. De capability van 1.67 is ruim boven de 1. Dat geeft ruimte voor kleine foutjes en versimpelingen die je mogelijk in je tolerantieanalyse hebt gemaakt. Vaak wordt een grens van 1.3 voor de capability gebruikt. Het geschatte uitvalpercentage geeft een nauwkeuriger beeld van de impact. De capability is erg handig om tolerantieketens onderling te vergelijken en om een uniforme eis voor tolerantieanalyses te stellen in je bedrijf.
Zelf oefenen?
Wil je zelf aan de slag met tolerantieanalyse? Neem dan dit voorbeeld en werk het uit waarbij je de kritische maat kiest voor de toestand ‘dicht’. Reken dan de ruimte tussen veerhouder E en de hefboom F uit. De nominale kritische maat is 0.5 mm, dat zagen we hierboven al. De te verwachten variatie is echter geen 0.833 mm, maar kleiner. Hoeveel?
Kom je er niet uit? Mail me dan gerust met een vraag.